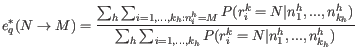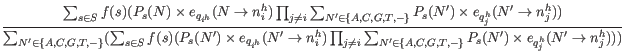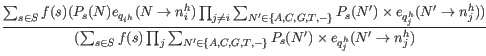Updating equations for the error rates
For the updating equations for the error probabilities, we consider a read,
Using Bayes formula again, as we did above in 31.4, we get:
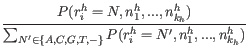 |
(31.8) |
and inserting the expression from equation 31.7:
The equation 31.9 gives us the probabilities for a given read, ![]() , and site,
, and site, ![]() , given the data
, given the data
![]() , that the true nucleotide is
, that the true nucleotide is ![]() ,
,
![]() , given our current values of the error rates and site probabilities. Since we know the sequenced nucleotide in each read at each site, we can get new updated values for the error rate of producing an
, given our current values of the error rates and site probabilities. Since we know the sequenced nucleotide in each read at each site, we can get new updated values for the error rate of producing an ![]() nucleotide when the true nucleotide is
nucleotide when the true nucleotide is ![]() ,
,
![]() , for
, for
![]() by summing the probabilities of the true nucleotide being
by summing the probabilities of the true nucleotide being ![]() for all reads across all sites for which the sequenced nucleotide is
for all reads across all sites for which the sequenced nucleotide is ![]() , and dividing by the sum of all probabilities of the true nucleotide being a
, and dividing by the sum of all probabilities of the true nucleotide being a ![]() across all reads and all sites:
across all reads and all sites: