Bioinformatics explained: Scoring matrices
Biological sequences have evolved throughout time and evolution has shown that not all changes to a biological sequence is equally likely to happen. Certain amino acid substitutions (change of one amino acid to another) happen often, whereas other substitutions are very rare. For instance, tryptophan (W) which is a relatively rare amino acid, will only -- on very rare occasions -- mutate into a leucine (L).
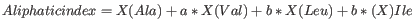 |
Based on evolution of proteins it became apparent that these changes or substitutions of amino acids can be modeled by a scoring matrix also refereed to as a substitution matrix. See an example of a scoring matrix in table 18.1. This matrix lists the substitution scores of every single amino acid. A score for an aligned amino acid pair is found at the intersection of the corresponding column and row. For example, the substitution score from an arginine (R) to a lysine (K) is 2. The diagonal show scores for amino acids which have not changed. Most substitutions changes have a negative score. Only rounded numbers are found in this matrix.
The two most used matrices are the BLOSUM [Henikoff and Henikoff, 1992] and PAM [Dayhoff and Schwartz, 1978].
Different scoring matrices
- PAM
The first PAM matrix (Point Accepted Mutation) was published in 1978 by Dayhoff et al. The PAM matrix was build through a global alignment of related sequences all having sequence similarity above 85% [Dayhoff and Schwartz, 1978]. A PAM matrix shows the probability that any given amino acid will mutate into another in a given time interval. As an example, PAM1 gives that one amino acid out of a 100 will mutate in a given time interval. In the other end of the scale, a PAM256 matrix, gives the probability of 256 mutations in a 100 amino acids (see figure 18.12).
There are some limitation to the PAM matrices which makes the BLOSUM matrices somewhat more attractive. The dataset on which the initial PAM matrices were build is very old by now, and the PAM matrices assume that all amino acids mutate at the same rate - this is not a correct assumption.
- BLOSUM
In 1992, 14 years after the PAM matrices were published, the BLOSUM matrices (BLOcks SUbstitution Matrix) were developed and published [Henikoff and Henikoff, 1992].
Henikoff et al. wanted to model more divergent proteins, thus they used locally aligned sequences where none of the aligned sequences share less than 62% identity. This resulted in a scoring matrix called BLOSUM62. In contrast to the PAM matrices the BLOSUM matrices are calculated from alignments without gaps emerging from the BLOCKS database.
Sean Eddy recently wrote a paper reviewing the BLOSUM62 substitution matrix and how to calculate the scores [Eddy, 2004].
Use of scoring matrices
Deciding which scoring matrix you should use in order of obtain the best alignment results is a difficult task. If you have no prior knowledge on the sequence the BLOSUM62 is probably the best choice. This matrix has become the de facto standard for scoring matrices and is also used as the default matrix in BLAST searches. The selection of a "wrong" scoring matrix will most probable strongly influence on the outcome of the analysis. In general a few rules apply to the selection of scoring matrices.
- For closely related sequences choose BLOSUM matrices created for highly similar alignments, like BLOSUM80. You can also select low PAM matrices such as PAM1.
- For distant related sequences, select low BLOSUM matrices (for example BLOSUM45) or high PAM matrices such as PAM250.
The BLOSUM matrices with low numbers correspond to PAM matrices with high numbers. (See figure 18.12) for correlations between the PAM and BLOSUM matrices. To summarize, if you want to find distant related proteins to a sequence of interest using BLAST, you could benefit of using BLOSUM45 or similar matrices.
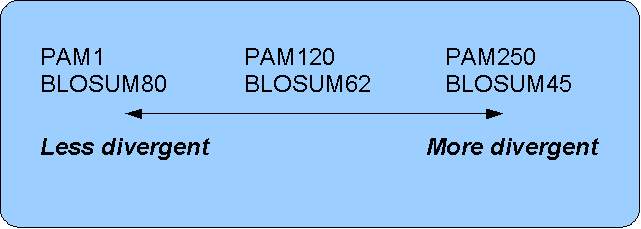
Figure 18.12: Relationship between scoring matrices. The BLOSUM62 has become a de facto standard scoring matrix for a wide range of alignment programs. It is the default matrix in BLAST.
