Hierarchical Clustering of Samples
A hierarchical clustering of samples is a tree representation of their relative similarity.
The tree structure is generated by
- letting each sample be a cluster
- calculating pairwise distances between all clusters
- joining the two closest clusters into one new cluster
- iterating 2-3 until there is only one cluster left (which will contain all samples).
(See [Eisen et al., 1998] for a classical example of application of a hierarchical clustering algorithm in microarray analysis. The example is on features rather than samples).
To start the clustering:
Tools | Microarray Analysis (![]() )| Quality Control (
)| Quality Control (![]() ) | Hierarchical Clustering of Samples (
) | Hierarchical Clustering of Samples (![]() )
)
Select a number of samples ( (![]() ) or (
) or (![]() )) or an experiment (
)) or an experiment (![]() ) and click Next.
) and click Next.
This will display a dialog as shown in figure 34.32. The hierarchical clustering algorithm requires that you specify a distance measure and a cluster linkage. The similarity measure is used to specify how distances between two samples should be calculated. The cluster distance metric specifies how you want the distance between two clusters, each consisting of a number of samples, to be calculated.
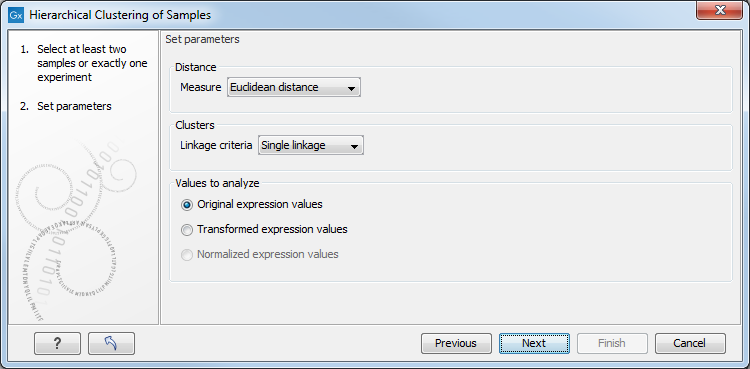
Figure 34.32: Parameters for hierarchical clustering of samples.
There are three kinds of distance measures:
- Euclidean distance. The length of the segment connecting two points. If
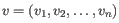 and
and
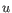 , then the Euclidean distance between
, then the Euclidean distance between 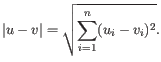 and
and 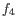 is
is
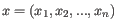
- Manhattan distance. The distance between two points measured along axes at right angles. If
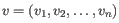 and
and
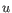 , then the Manhattan distance between
, then the Manhattan distance between 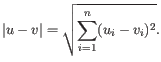 and
and 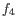 is
is
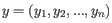
- 1 - Pearson correlation. The Pearson correlation coefficient between
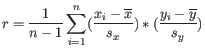 and
and
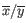 is defined as
where
is defined as
where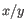
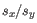 and
and 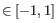 are the average and sample standard deviation, respectively, of the values in
are the average and sample standard deviation, respectively, of the values in 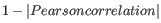 values.
values.
The Pearson correlation coefficient ranges from -1 to 1, with high absolute values indicating strong correlation, and values near 0 suggesting little to no relationship between the elements.
Using 1 - | Pearson correlation | as the distance measure ensures that highly correlated elements have a shorter distance, while elements with low correlation are farther apart.
The distance between two clusters is determined using one of the following linkage types:
- Single linkage. The distance between the two closest elements in the two clusters.
- Average linkage. The average distance between elements in the first cluster and elements in the second cluster.
- Complete linkage. The distance between the two farthest elements in the two clusters.
At the bottom, you can select which values to cluster (see Selecting transformed and normalized values for analysis).
Click on Finish to launch the analysis.
Note: To be run on a server, the tool has to be included in a workflow, and the results will be displayed in a a stand-alone new heat map rather than added into the input experiment table.
Subsections
