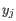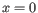The GLM model

Fitting a GLM to expression data

It is easiest to understand how the GLM model works through an example. Imagine an experiment looking at the effect of two drug treatments while controlling for gender:

In an abuse of mathematical notation, the underlying GLM for each gene looks like

$\displaystyle \log{y_i} = \mathrm{(placebo and Male)} + \mathrm{drugA} + \mathrm{drugB} + \mathrm{Female} + \mathrm{constant_i}$

where $ y_i$ is the expression level for the gene in sample $ i$; the combined term $ \mathrm{(placebo and Male)}$ describes an arbitrarily chosen baseline expression level (of males being given a placebo); and the other terms $ \mathrm{drugA}$, $ \mathrm{drugB}$ and $ \mathrm{Female}$ are numbers describing the effect of each group with respect to this baseline. The $ \mathrm{constant_i}$ accounts for differences in the library size between samples. For example, if a subject is male and given a placebo we predict the expression level to be

$\displaystyle \log{y_i} = \mathrm{(placebo and Male)} + \mathrm{constant_i}.$

If instead he had been given drug B, we would predict the expression level $ y_i$ to be augmented with the $ \mathrm{drugB}$ coefficient, resulting in

$\displaystyle \log{y_i} = \mathrm{(placebo and Male)} + \mathrm{drugB} + \mathrm{constant_i}.$

We assume that the expression levels $ y_i$ follow a Negative Binomial distribution. This distribution has a free parameter, the dispersion. The greater the dispersion, the greater the variation in expression levels for a gene.

The most likely values of the dispersion and coefficients, $ \mathrm{drugA}$, $ \mathrm{drugB}$ and $ \mathrm{Female}$, are determined simultaneously by fitting the GLM to the data. To see why this simultaneous fitting is necessary, imagine an experiment where we observe counts {15,10,4} for Males and {30,20,8} for Females. The most natural fit is for the coefficient $ \mathrm{Female}$ to have a two-fold change and for the dispersion to be small, but an alternative fit has no fold change and a larger dispersion. Under this second fit the variation in the counts is greater, and it is just by chance that all three Female values are larger than all three Male values.

Refining the estimate of dispersion

Much research has gone into refining the dispersion estimates of GLM fits. One important observation is that the GLM dispersion for a gene is often too low, because it is a sample dispersion rather than a population dispersion. We correct for this using the Cox-Reid adjusted likelihood, as in the multi-factorial edgeR method [Robinson et al., 2010]. To understand the purpose of the correction, it may help to consider the analogous situation of calculation of the variance of normally distributed measurements. One approach would be to calculate $ \frac{1}{n} \sum(x_i - \overline{x})^2$, but this is the sample variance and often too low. A commonly used correction for the population variance is: $ \frac{1}{n-1} \sum (x_i - \overline{x})^2$.

A second observation that can be used to improve the dispersion estimate, is that genes with the same average expression often have similar dispersions. To make use of this observation, we follow [Robinson et al., 2010] in estimating gene-wise dispersions from a linear combination of the likelihood for the gene of interest and neighboring genes with similar average expression levels. The weighting in this combination depends on the number of samples in an experiment, such that the neighbors have most weight when there are no replicates, and little effect when the number of replicates is high.

When estimating dispersion, we use the following strategy:

  1. We sort the genes from lowest to highest average logCPM (CPM is defined also by the edgeR authors). For each gene, we calculate its log-likelihood at a grid of known dispersions. The known dispersions are 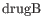$ 0.2 * 2^i$, where 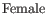$ i = { -6, -4.8, -3.6... 6 }$ such that there are 11 values of i in total. You can imagine the results of this as being stored in a table with one column for each gene and one row for each dispersion, with neighboring columns having similar average logCPM (because of the sorting in the previous step).

  2. We now calculate a weighted log-likelihood for each gene at these same known dispersions. This is the original log-likelihood for that gene at that dispersion plus a "weight factor" multiplied by the average log-likelihood for genes in a window of similar average logCPM. The window includes the 1.5% of genes to the left and to the right of the gene we are looking at. For example, if we had 3000 genes, and were calculating values for gene 500, then 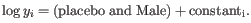$ 0.015*3000 = 45$, so we would average the values for genes 455 to 545. The "weight factor" = 20 / (numberOfSamples - number of parameters in the factor being tested). This means that the greater the number of samples, the lower the weight, and the fewer free parameters to fit, the lower the weight.

  3. We fit an FMM spline for each gene to its 11 weighted log-likelihoods. Our implementation of the FMM spline is translated from the Fortran code found here http://www.netlib.org/fmm/spline.f. This spline allows us to estimate the weighted log-likelihood at any dispersion within the grid i.e., from $ 0.2 * 2^{-6}$ to $ 0.2*2^6$

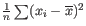
  4. We find the dispersion on the spline that maximizes the log-likelihood. This is the dispersion we use for that gene.

Downweighting outliers

It is often difficult to detect outliers. Therefore, instead of removing putative outliers completely from the GLM fit, we give them "observation weights" that are smaller than 1. These weights reduce the effect of the outliers on the GLM fit.

Outliers can have two undesirable effects. First, genes with outliers are more likely to be called as differentially expressed because a sample with anomalously high expression is hard to reconcile with no fold change. Second, outliers can prevent differentially expressed genes from being detected. This is because, when a gene has an anomalously high expression, the dispersion for that gene will typically be overestimated. Consequently the dispersion of genes with similar expression will be overestimated, such that they are less likely to be called as differentially expressed.

When downweighting outliers, the above dispersion estimation procedure is repeated 5 more times, and per-gene weights are estimated for the samples at each iteration. Note that these weights are not related to the weights in the weighted log-likelihood of the dispersion estimation procedure.

The following iterative procedure is performed to estimate the observation weights. For each gene, one iteration proceeds as follows:

  1. The Cook's distance is calculated for each sample. The Cook's distance for sample $ i$ is

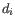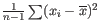
    $\displaystyle D_i = \frac{1}{p} {z_i}^2 \frac{h_i}{(1-h_i)^2} $

    where
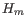    • $ p$ is the number of parameters in the fit.
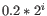    • $ z_i$ is the Pearson residual for sample 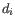$ i$, a measure of how well the fitted model predicts the expression of sample 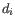$ i$. The Pearson residual is calculated as the difference between the measured expression 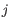$ y_i$ and the modeled expression 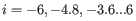$ \hat{y_i}$, divided by the standard deviation 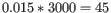$ \sigma$ of the negative binomial distribution with dispersion 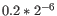$ \gamma$ that has been fitted to the gene:

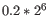
      $\displaystyle z_i = \frac{y_i - \hat{y_i}}{\sigma} = \frac{y_i - \hat{y_i}}{\sqrt{\hat{y_i}(1+\gamma\hat{y_i})}} $

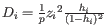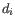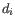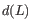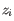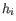    • $ h_i$ is the leverage of sample $ i$ on the fit, a measure of how much sample $ i$ affects the fitted parameters. The leverage is the $ i^{th}$ entry on the diagonal of the projection matrix $ H$ which relates measured expressions to modeled expressions: $ \hat{y_i} = H y_i$.

    Outliers are expected to have large Cook's distances because they tend to be poorly fitted, resulting in large 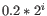$ z_i$, and they are likely to disproportionately influence the fit compared to other points, leading to large $ h_i$.

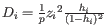  2. Cook's distances are assumed to follow an F distribution 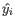$ F(p, n-p)$, where 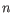$ n$ is the number of samples. For each sample, this distribution is used to calculate the probability 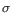$ p(D_i)$ of obtaining a Cook's distance as extreme as or more extreme than the observed 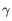$ D_i$. A first approximation for the sample observation weight is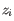 $ w_i$

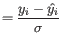
    $\displaystyle w_i = \left\{ \begin{array}{ll} p(D_i) & \mbox{if } p(D_i) < 0.5 \\ 1 & \mbox{otherwise} \end{array}\right. $

    The probability cut-off of 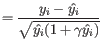$ 0.5$ is set empirically from experiments on real data.

  3. This approximation is not effective in practice when outliers are present because a single outlier in a condition can influence the fit for all other samples within that condition, causing them to also exhibit large Cook's distances and appear as outliers. As a result, this approximation leads to reduced observation weights of many non-outlier samples, especially during the initial iteration of the procedure. We address this in two parts:

    1. We limit how much a group of samples is downweighted. For the example at the start of this section, the groups are "drug A female", "drug A male", "drug B female" etc. The allowed downweighting for a group 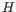$ g$ containing 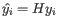$ n_g$ samples is:

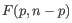
      $\displaystyle d_g = \min \left( \sum_{i \in g} 1 - w_i, \min \Bigl( n_g - 1, \max(1, 0.1 n_g) \Bigr) \right) $

      We hence disregard at most one sample or up to 10% of the samples from the group, whichever is larger. However, at least one sample from the group must be kept. In practice, the weights are spread across all samples: while some samples may be more heavily downweighted than others, it is uncommon for any sample to be entirely ignored, i.e., receive an observation weight 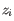$ w_i$ of 0.

    2. We calculate a normalized skewed weight

      $\displaystyle s_i = \left\{ \begin{array}{ll} \frac{1}{s_t} \frac{w_{min}}{w_i} & \mbox{if } p(D_i) < 0.5 \\ 0 & \mbox{otherwise} \end{array} \right. $

      to penalize the most extreme outliers, where
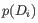
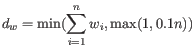      • $ w_{min}$ is the smallest 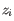$ w_i$ across all samples, regardless of their group.
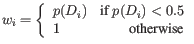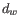      • $ s_t$ is the normalization factor such that $ \sum_k s_k = 1$.

      If the true outlier has a 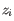$ w_i$ that is 10 times smaller than another sample in the same group, then 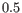$ s_i$ for the true outlier will also be 10 times smaller than the one for the other sample.

  4. The final observation weights are:

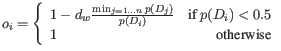
    $\displaystyle o_i = 1 - \min \left( 1, \gamma d_g s_i \right) $

    where 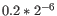$ \gamma$ is a normalization factor used to ensure that at most one sample, or 10% of the total number of samples 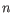$ n$ are disregarded from the entire dataset:

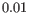
    $\displaystyle \gamma = \min \left( 1, \frac{\max(1, 0.1 n)}{\sum_i \min (1, d_g s_i)} \right) $

  5. The GLM is re-fit, using these weights.

The above steps are repeated until no observation weight changes by more than $ 0.01$, or a weight that was $ <0.01$ becomes 1 in the following round, or a weight that decreased by more than $ 0.01$ in the previous round increases by more than $ 0.01$ in the next round. These stopping criteria are needed because the weights do not converge: when a weight becomes sufficiently small, the leverage component of the Cook's distance tends to zero and so the Cook's distance also becomes zero and the weight in the next iteration will be 1.

Once the observation weights have been determined, the re-fitted GLM has a different likelihood than before. This is partly because the weighting is applied directly to the likelihood, and partly because the weighting affects the fitted coefficients.

The use of observation weights in the GLM is based on [Zhou et al., 2014]. The use of Cook's distance is motivated by DESeq2, which ignores genes with extreme Cook's distances when the number of replicates is small, rather than downweighting them. The form of the weights is novel to CLC Genomics Workbench.

Statistical testing

The final GLM fit and dispersion estimate allows us to calculate the total likelihood of the model given the data, and the uncertainty on each fitted coefficient. The two statistical tests each make use of one of these values.

Wald test
Tests whether a given coefficient is non-zero. This test is used in the All group pairs and Against control group comparisons. For example, to test whether there is a difference between subjects treated with a placebo, and those treated with drugB, we would use the Wald test to determine if the 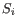$ \mathrm{drugB}$ coefficient is non-zero.
Likelihood Ratio test
Fits two GLMs, one with the given coefficients and one without. The more important the coefficients are, the greater the ratio of the likelihoods of the two models. The likelihood of both models is computed using the dispersion estimate and observation weights of the larger model. This test is used in the Across groups (ANOVA-like) comparison. If we wanted to test whether either drug had an effect, we would compare the likelihoods of the GLM described with equation

$\displaystyle \log{y_i} = \mathrm{(placebo and Male)} + \mathrm{drugA} + \mathrm{drugB} + \mathrm{Female} + \mathrm{constant_i}$

with those in the reduced GLM with equation

$\displaystyle \log{y_i} = \mathrm{(Male)} + \mathrm{Female} + \mathrm{constant_i} .$