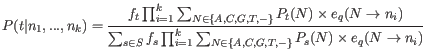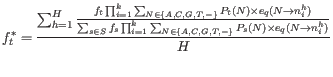Updating equations for the prior site type probabilities
We first derive the updating equations for the prior site type probabilities
Now, for ![]() we use our current value for
we use our current value for ![]() , and if we further insert the expression for
, and if we further insert the expression for
![]() (31.2) we get:
(31.2) we get:
We get the updating equation for the prior site type probabilities,
![]() , from equation 31.5: Let
, from equation 31.5: Let ![]() index the sites in the alignment (
index the sites in the alignment (![]() ). Given the current values for the set of site frequencies,
). Given the current values for the set of site frequencies,
![]() , and the current values for the set of error probabilities, we obtain updated values for the site frequencies,
, and the current values for the set of error probabilities, we obtain updated values for the site frequencies,
![]() , by summing the site type probabilities given the data (as given by equation 31.5) across all sites in the alignment:
, by summing the site type probabilities given the data (as given by equation 31.5) across all sites in the alignment: