The CLC de novo assembly algorithm
Our de novo assembly algorithm works by using de Bruijn graphs. This is a common approach used with de novo assembly algorithms described in [Zerbino and Birney, 2008,Zerbino et al., 2009,Li et al., 2010,Gnerre et al., 2011]. The basic idea is to make a table of all sub-sequences of a certain length (called words) found in the reads. The words are relatively short, e.g. about 20 for small data sets and 27 for a large data set. In the following section, we use the term word size to denote the length of a word. The word size is by default determined automatically (see explanation below).
Given a word in the table, we can look up all the potential neighboring words (in all the examples here, word of length 16 are used) as shown in figure 30.1.

Figure 30.1: The word in the middle is 16 bases long, and it shares the 15 first bases with the backward neighboring word and the last 15 bases with the forward neighboring word.
Typically, only one of the backward neighbors and one of the forward neighbors will be present in the table. A graph can then be made where each node is a word that is present in the table and edges connect nodes that are neighbors. This is called a de Bruijn graph.
For genomic regions without repeats or sequencing errors, we get long linear stretches of connected nodes. We may choose to reduce such stretches of nodes with only one backward and one forward neighbor into nodes representing sub-sequences longer than the initial words.
Figure 30.2 shows an example where one node has two forward neighbors:

Figure 30.2: Three nodes connected, each sharing 15 bases with its neighboring node and ending with two forward neighbors.
After reduction, the three first nodes are merged, and the two sets of forward neighboring nodes are also merged as shown in figure 30.3.

Figure 30.3: The five nodes are compacted into three. Note that the first node is now 18 bases and the second nodes are each 17 bases.
So bifurcations in the graph leads to separate nodes. In this case we get a total of three nodes after the reduction. Note that neighboring nodes still have an overlap (in this case 15 nucleotides since the word size is 16).
Given this way of representing the de Bruijn graph for the reads, we can consider some different situations:
When we have a SNP or a sequencing error, we get a so-called bubble (this is explained in detail in Bubble resolution) as shown in figure 30.4.

Figure 30.4: A bubble caused by a heterozygous SNP or a sequencing error.
Here, the central position may be either a C or a G. If this was a sequencing error occurring only once, it would be represented in the bubble as a path that is associated with a word that only occurs a single time'. On the other hand if this was a heterozygous SNP we would see both paths represented more or less equally in terms of the number of words that support each path. Thus, having information about how many times this particular word is seen in all the reads is very useful and this information is stored in the initial word table together with the words.
The most difficult problem for de novo assembly is repeats. Repeat regions in large genomes often get very complex: a repeat may be found thousands of times and part of one repeat may also be part of another repeat. Sometimes a repeat is longer than the read length (or the paired distance when pairs are available) and then it becomes impossible to resolve the length of the repeat. This is simply because there is no information available about how to connect the nodes before the repeat to the nodes after the repeat, and we just do not know how long the repeat is.
In the simple example, if we have a repeat sequence that is present twice in the genome, we would get a graph as shown in figure 30.5.
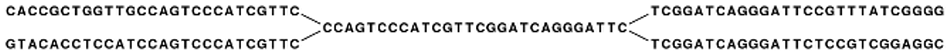
Figure 30.5: The central node represents the repeat region that is represented twice in the genome. The neighboring nodes represent the flanking regions of this repeat in the genome.
Note that this repeat is 57 nucleotides long (the length of the sub-sequence in the central node above plus regions into the neighboring nodes where the sequences are identical). If the repeat had been shorter than 15 nucleotides, it would not have shown up as a repeat at all since the word size is 16. This is an argument for using long words in the word table. On the other hand, the longer the word, the more words from a read are affected by a sequencing error. Also, for each increment in the word size, we get one less word from each read. This is in particular an issue for very short reads. For example, if the read length is 35, we get 16 words out of each read if the word size is 20. If the word size is 25, we get only 11 words from each read.
To strike a balance, our de novo assembler chooses a word size based on the amount of input data: the more data, the longer the word length. It is based on the following:
word size 12: 0 bp - 30000 bp word size 13: 30001 bp - 90002 bp word size 14: 90003 bp - 270008 bp word size 15: 270009 bp - 810026 bp word size 16: 810027 bp - 2430080 bp word size 17: 2430081 bp - 7290242 bp word size 18: 7290243 bp - 21870728 bp word size 19: 21870729 bp - 65612186 bp word size 20: 65612187 bp - 196836560 bp word size 21: 196836561 bp - 590509682 bp word size 22: 590509683 bp - 1771529048 bp word size 23: 1771529049 bp - 5314587146 bp word size 24: 5314587147 bp - 15943761440 bp word size 25: 15943761441 bp - 47831284322 bp word size 26: 47831284323 bp - 143493852968 bp word size 27: 143493852969 bp - 430481558906 bp word size 28: 430481558907 bp - 1291444676720 bp word size 29: 1291444676721 bp - 3874334030162 bp word size 30: 3874334030163 bp - 11623002090488 bp etc.This pattern (multiplying by 3) continues until word size of 64 which is the max. See how to adjust the word size in De novo assembly parameters
Subsections
- Resolve repeats using reads
- Automatic paired distance estimation
- Optimization of the graph using paired reads
- AGP export
- Bubble resolution
- Converting the graph to contig sequences
- Summary
