Predict Methylation Profile
The Predict Methylation Profile tool estimates the composition of an input sample. The tool is primarily designed for use with the QIAseq Targeted Methyl panel "T Cell Infiltration Panel (MHS-202Z)", though it can be used in other settings.
To start the tool, go to:
Tools | Epigenomics Analysis (![]() ) | Bisulfite Sequencing (
) | Bisulfite Sequencing (![]() )| Predict Methylation Profile (
)| Predict Methylation Profile (![]() )
)
In the first dialog, choose a methylation levels track produced by the tool Call Methylation Levels. It is recommended that the Call Methylation Levels tool has been run with the option to Report unmethylated cytosines. Click Next to configure the following parameters:
- Reference
- Methylation database An annotation track containing, for each region, known methylation levels in the range
![$ [0,1]$](img59.gif) for a 'pure' sample of a given type. There is no limit on the number of pure types that can be used, but prediction becomes more difficult as more types are added. Regions can be a single cytosine, a two nucleotide long CpG site, or a longer stretch of cytosines. When using longer stretches of cytosines, note that there are multiple ways of defining the known methylation level - for example, two ways might be as the arithmetic mean of the included cytosines, or the geometric mean. Best results will be obtained when the known methylation levels are defined as described for Case methylation level or Control methylation level in Call Methylation Levels
for a 'pure' sample of a given type. There is no limit on the number of pure types that can be used, but prediction becomes more difficult as more types are added. Regions can be a single cytosine, a two nucleotide long CpG site, or a longer stretch of cytosines. When using longer stretches of cytosines, note that there are multiple ways of defining the known methylation level - for example, two ways might be as the arithmetic mean of the included cytosines, or the geometric mean. Best results will be obtained when the known methylation levels are defined as described for Case methylation level or Control methylation level in Call Methylation Levels
- Known methylation level columns The names of columns within the Methylation database annotation track that refer to known methylation levels. The default values of "Epi", "Fib", and "IC", are chosen to match reference data distributed for the T Cell Infiltration Panel. These only need to be changed when a custom Methylation database is used.
- Methylation database An annotation track containing, for each region, known methylation levels in the range
- Filtering
- Minimum coverage Regions are removed if their average coverage per cytosine present in the input methylation levels track is lower than this.
- Merge nearby regions Methylation levels are often highly-correlated over short regions of the genome. Prediction works best when the input regions provide independent information about methylation. If two regions are closer than
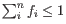 nt, and they appear to have compatible methylation levels, and this option is enabled, then they will be merged into a single region.
nt, and they appear to have compatible methylation levels, and this option is enabled, then they will be merged into a single region.
Constructing a custom methylation database
A database of two or three pure types can be created by using the Create Methylation Database tool described in Create Methylation Database. Another option is to import a custom methylation database from an annotation file format such as GFF3, GTF, or BED, using Import | Tracks.
An example of a database with two pure types, "mcf" and "leuko", is provided in tab-delimited GFF3 format below. For more details of the format, refer to https://github.com/The-Sequence-Ontology/Specifications/blob/master/gff3.md
##gff-version 3.1.26 1 . sequence_feature 3567263 3567264 . . . mcf=0.11;leuko=0.95 1 . sequence_feature 3567272 3567273 . . . mcf=0.16;leuko=1 1 . sequence_feature 3567288 3567289 . . . mcf=0.2;leuko=0.99 ...
Note that every region must be annotated with every pure type - in the above example, the tool would skip regions that only had information for "mcf" and not "leuko". Also be sure to check that the imported coordinates match your expectations. This is easily done when the regions in the database are CpG sites, by making a new Track List of the reference track and the imported database.
When constructing a custom methylation database it is important to avoid bias. This can take different forms.
- Bias in methylation level Imagine a database where there are two pure types, "Epithelial cells" and "Blood", defined such that regions are always hypomethylated in epithelial cells and hypermethylated in blood. Then a sample with a generally high methylation will be classified as blood with high confidence. If instead the database had a mixture of hypermethylated regions for both pure types, then we might find that the same sample was predicted uncertainly with large confidence intervals.
- Bias in the number of regions informative for each type Imagine a database of three types "Epithelial cells", "Fibroblast cells", and "Immune cells", where regions are chosen for being able to distinguish one type from the other two. In this setup, there are three kinds of regions: those useful for distinguishing "Epithelial cells vs Fibroblast cells", "Epithelial cells vs Immune cells", or "Fibroblast cells vs Immune cells". If there are only few regions to distinguish "Fibroblast cells vs Immune cells" then the confidence intervals for these two types will likely be much larger than for epithelial cells.
The Predict Methylation Profile algorithm
The algorithm splits an input sample into a mixture of the types listed in the Known methylation level columns parameter. If there are ![]() such types, then we define the fraction that is of type
such types, then we define the fraction that is of type ![]() to be
to be ![]() and impose the constraints
and impose the constraints
![]() ,
,
![]() .
.
The regions of the methylation database are first filtered to remove regions whose coverage is lower than specified in the Minimum coverage option.
If the option Merge nearby regions is enabled, then the remaining regions are merged if they meet all the following conditions:
- They are separated on the genome by
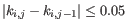 nt with no other region between them.
nt with no other region between them.
- The known methylation levels,
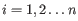 for pure type
for pure type 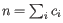 and the two adjacent regions
and the two adjacent regions 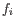 and
and 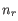 satisfy
satisfy
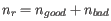 ,
,
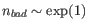
- The 95% confidence intervals of the methylation levels of the two regions overlap. The intervals are calculated using the Wilson score interval.
The ![]() merged regions are then used for prediction using a maximum likelihood approach. In the underlying model, regions can be "good" regions or "bad" regions, such that
merged regions are then used for prediction using a maximum likelihood approach. In the underlying model, regions can be "good" regions or "bad" regions, such that
![]() . The predicted composition is only consistent with the methylation levels of the good regions.
. The predicted composition is only consistent with the methylation levels of the good regions.
The total number of bad regions is exponentially distributed to ensure that predictions requiring many bad regions are disfavored. Specifically,
![]() . This means that the number of bad regions is a free parameter (though bound such that
. This means that the number of bad regions is a free parameter (though bound such that
![]() ) that must be determined at the same time as the sample compositions. This explicit modeling of bad regions reflects the observation that not all regions in the database will generalize to new samples as the methylation database is constructed from a limited number of samples.
) that must be determined at the same time as the sample compositions. This explicit modeling of bad regions reflects the observation that not all regions in the database will generalize to new samples as the methylation database is constructed from a limited number of samples.
For a given prediction, ![]() ,
,
![]() , the expected methylation level at site
, the expected methylation level at site ![]() is
is
![]()
The likelihood of a region with ![]() methylated reads and coverage
methylated reads and coverage ![]() being good is binomially distributed:
being good is binomially distributed:
| (10.1) |
All bad regions have the same likelihood, ![]() , which is a uniform distribution over the total number of regions,
, which is a uniform distribution over the total number of regions, ![]() :
:
| (10.2) |
The bad regions that maximize the log-likelihood for a given prediction ![]() ,
,
![]() are found by ordering regions by
are found by ordering regions by
![]() in ascending order. Then up to the first
in ascending order. Then up to the first ![]() regions with
regions with
![]() are bad regions.
are bad regions.
The total log-likelihood for a given prediction is then:
| log-likelihood |
(10.3) |
The prediction maximizing the total log-likelihood is found by numerical optimization.
95% confidence intervals for ![]() are estimated by taking the 5th percentile and 95th percentile values calculated from
are estimated by taking the 5th percentile and 95th percentile values calculated from ![]() bootstrap iterations. In each iteration, the same number of regions as used for the initial prediction are randomly chosen with replacement from the list of regions used for that prediction, and the prediction is re-calculated on these.
bootstrap iterations. In each iteration, the same number of regions as used for the initial prediction are randomly chosen with replacement from the list of regions used for that prediction, and the prediction is re-calculated on these.
The Predict Methylation Profile report
The predict methylation profile report includes the following information:
- Summary
- Total regions The number of regions in the methylation database.
- Regions with too few counts The number of regions removed by the Low coverage option.
- Regions not used Of the remaining regions, the number that were classed as "bad" regions, and so were not used to estimate the composition of the input sample.
- Regions used Regions that had sufficient coverage and were classed as "good" regions, and so were used to estimate the composition of the input sample.
- Merged regions used The number of good regions after merging nearby regions. This row is only shown when Merge nearby regions is enabled.
- Results One row is shown for each type specified by the Known methylation level columns option.
- Cell type The name of the type.
- Percentage The percentage of the sample estimated to come from the given type.
- 95% CI A 95% confidence interval for the estimated percentage.
Note that the 95% confidence intervals only approximate the error due to the prediction being based on a selection of a small number of regions of the genome. Additional sources of error include:
- The uncertainty in each of the provided known methylation levels in the methylation database. This uncertainty can be minimized by using sites/regions with high coverage, and by validating them in many 'pure' samples.
- The presence of types in the sample that are not listed in the known methylation level columns.
- Bias in the construction of the methylation database.
As a rule-of-thumb, one should suspect the presence of these additional sources of error when
![]() .
.
The Predict Methylation Profile region track
The columns of the predict methylation profile region track indicate:
- Name the name of the region in the Methylation database
- Group a number showing how regions are grouped by the Merge nearby regions option. If the option is disabled then each region will have a different number. Otherwise regions within
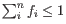 nt of each other with compatible methylation levels will share a number, indicating that they were merged into one region during prediction.
nt of each other with compatible methylation levels will share a number, indicating that they were merged into one region during prediction.
- <Known methylation level columns> One column for each of the known methylations supplied to the tool.
- Total methylated coverage The sum of the coverage of all input methylated cytosines within the region.
- Total context coverage The sum of the coverage of all input cytosines within the region.
- Number of cytosines The number of input cytosines within the region for which methylation was reported. Note that the number of input cytosines is often smaller than the number of cytosines in the genome for the same region, for example because there is no read coverage at some positions.
- Observed methylation level The Total methylated coverage divided by the Total context coverage.
- Predicted methylation level The expected methylation level calculated by multiplying the predicted sample composition by the values in the <Known methylation level columns>. For example, if there are three such columns "Epi = 0.3", "Fib = 0.6" and "IC = 0.1", and the tool predicts that the sample is 50% Epi and 50% IC, then this value will be 0.5 x 0.3 + 0 x 0.6 + 0.5 x 0.1 = 0.2.
- Low coverage Whether the region was filtered away by the Minimum coverage option.
- Used Whether the region was predicted to be a "good" region i.e. not a "bad" region. Typically bad regions have large differences between the Observed methylation level and the Predicted methylation level.
