Create UMI Reads from Grouped Reads
The tool Create UMI Reads from Grouped Reads generates a single consensus read, called a UMI read, from reads which belong to the same group, as determined by the Calculate Unique Molecular Index Groups tool. The consensus reads are placed in a read mapping at the location of the original reads. Therefore, the output of the tool is a read mapping of generated UMI reads.
The tool can be found in the Toolbox here:
Toolbox | Biomedical Genomics Analysis (
) | UMI Tools (
) | Create UMI Reads from Grouped Reads (
)
In the first dialog (figure 4.4), select a read mapping of the original reads with UMI annotations that was previously handled with the Calculate Unique Molecular Index Groups tool.
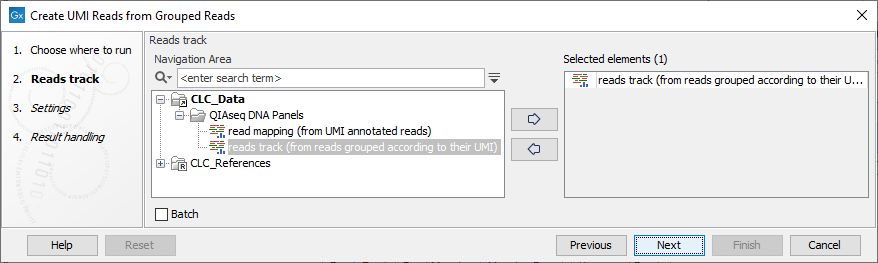
Figure 4.4: Select a read mapping of the original reads with UMI annotations.
The second dialog of the wizard (figure 4.5) offers the following options:
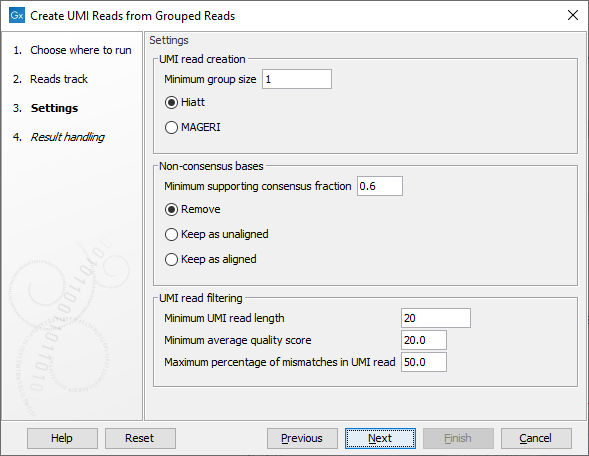
Figure 4.5: Settings for the Create UMI Reads from Grouped Reads tool.
- UMI read creation
- Minimum group size: The tool will only create a UMI read if the number of reads in the UMI is at least "Minimum group size".
- Quality score calculation method: Choose between two methods for computing Q-scores for UMI consensus reads (for more details see Consensus Q-score):
- Hiatt: The Q-score is calculated following the method described in [Hiatt et al., 2013].
The quality score is
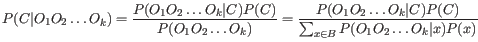of the posterior probability of the consensus base.
- MAGERI: The Q-score is calculated using a slightly modified version of the method described in [Shugay et al., 2017].
- Hiatt: The Q-score is calculated following the method described in [Hiatt et al., 2013].
The quality score is
- Non-consensus bases
- Minimum supporting consensus fraction set at 0.6 by default. At each position in the UMI read, the consensus nucleotide is chosen to be the nucleotide with the highest probability of being correct (see the Consensus nucleotide calculation paragraph below). If this probability is higher than "Minimum supporting consensus fraction", a Q score for the consensus nucleotide is calculated. A position in UMI reads that does not have a consensus nucleotide will be considered a N with Q score 0.
- There is a choice between 3 methods of handling non-consensus bases (N with a Q score of 0) that are located at the end of the reads: Remove removes the bases, Keep as unaligned keeps the bases as unaligned ends, and Keep as aligned keeps the bases as aligned bases.
- UMI read filtering
- Minimum UMI read length: UMI shorter than this value will be discarded.
- Minimum average quality score: UMI reads will be discarded, if their average Q-score is lower than "Minimum average quality score".
- Maximum percentage of mismatches in UMI read: UMI reads will be discarded, if more than this percentage of the bases are mismatches.
Click Next to Open or Save the resulting read mapping of UMI reads, i.e., a read mapping of the merged UMI groups. UMI reads are named umi[UMI_ID]_count[UMI_group_size], where UMI_ID is a unique UMI group number, and UMI_group_size is the number of reads that are in that UMI group.
It is also possible to generate a report that will indicate how many reads were ignored and the reason why they were not included in a UMI read.
Subsections