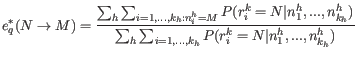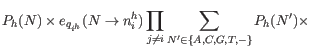Updating equations for the error rates
For the updating equations for the error probabilities we use the same procedure as for the Fixed Ploidy variant caller: We will use equation 27.7, however, in the case of the Low Frequency variant caller we do not have prior site type probabilities but instead have Maximum Likelihood estimates of the fractions of each nucleotide at the sites under the currently favored Multinomial model for that site. Let ![]() be the frequency of the nucleotide
be the frequency of the nucleotide ![]() at site
at site ![]() as determined by our current Maximum Likelihood estimates for these. Consider a read,
as determined by our current Maximum Likelihood estimates for these. Consider a read, ![]() , at a given site,
, at a given site, ![]() . The joint probability of the true nucleotide in the read,
. The joint probability of the true nucleotide in the read, ![]() , at the site being
, at the site being ![]() and the data
and the data
![]() :
:
As for the Fixed Ploidy variant caller we use Bayes formula to get:
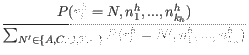 |
and insert the expression from equation 27.10 to get:
We calculate the
![]() values in equation 27.12, using our current error estimates and our current Maximum likelihood values of the frequencies for our current multinomial models of choice at each of the sites. We then use these to get new updated values for the error rates in a manner similar to that of the Fixed Ploidy Variant Caller we use the equation:
values in equation 27.12, using our current error estimates and our current Maximum likelihood values of the frequencies for our current multinomial models of choice at each of the sites. We then use these to get new updated values for the error rates in a manner similar to that of the Fixed Ploidy Variant Caller we use the equation: