Resolve repeats without conflicts

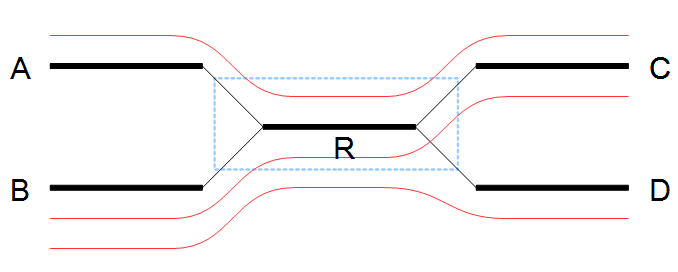
Repeats and other shared regions between the reads lead to ambiguities in the graph. These must be resolved otherwise the region will be output as multiple contigs, one for each node in the region.

The algorithm for resolving repeats without conflicts considers a number of nodes called the window. To start with, a window only contains one node, say R. We also define the border nodes as the nodes outside the window connected to a node in the window. The idea is to divide the border nodes into sets such that border nodes A and C are in the same set if there is a read going through A, through nodes in the window and then through C. If there are strictly more than one of these sets we can resolve the repeat area, otherwise we expand the window.

Image read_opt_1
Figure 28.6: A set of nodes.

In the example in figure 28.6 all border nodes A, B, C and D are in the same set since one can reach every border nodes using reads (shown as red lines). Therefore we expand the window and in this case add node C to the window as shown in figure 28.7.

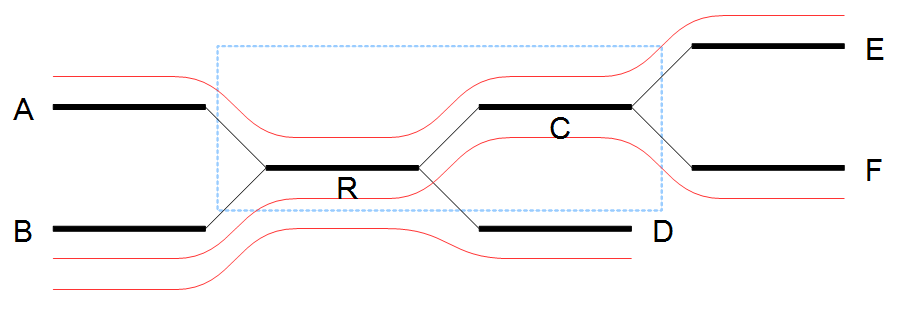
Image read_opt_2
Figure 28.7: Expanding the window to include more nodes.

After the expansion of the window, the border nodes will be grouped into two groups being set A, E and set B, D, F. Since we have strictly more than one set, the repeat is resolved by copying the nodes and edges used by the reads which created the set. In the example the resolved repeat is shown in figure 28.8.

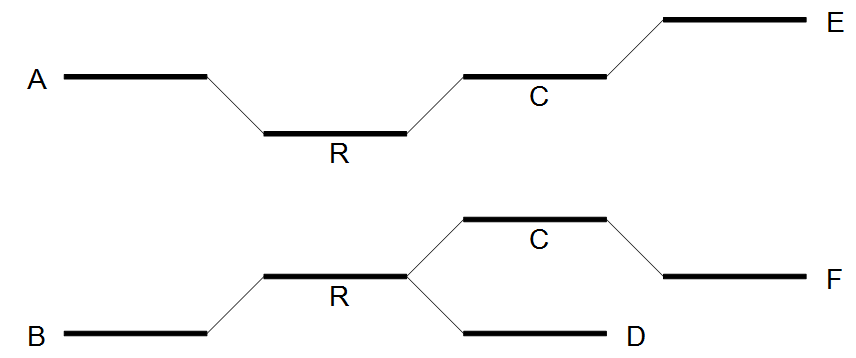
Image read_opt_5
Figure 28.8: Resolving the repeat.

The algorithm for resolving repeats without conflict can be described the following way:

  1. A node is selected as the window
  2. The border is divided into sets using reads going through the window. If we have multiple sets, the repeat is resolved.
  3. If the repeat cannot be resolved, we expand the window with nodes if possible and go to step 2.
The above steps are performed for every node.