Resolve repeats with conflicts

In the previous section repeats were resolved without excluding any reads that goes through the window. While this lead to a simpler graph, the graph will still contain artifacts, which have to be removed. The next phase removes most of these errors and is similar to the previous phase:
  1. A node is selected as the initial window
  2. The border is divided into sets using reads going through the window. If we have multiple sets, the repeat is resolved.
  3. If the repeat cannot be resolved, the border nodes are divided into sets using reads going through the window where reads containing errors are excluded. If we have multiple sets, the repeat is resolved.
  4. The window is expanded with nodes if possible and step 2 is repeated.

The algorithm described above is similar to the algorithm used in the previous section, except step 3 where the reads with errors are excluded. This is done by calculating an average $ avg_1 = m_1 / c_1$ where $ m_1$ is the number of reads going through the window and $ c_1$ is the number of distinct pairs of border nodes having one (or more) of these reads connecting them. A second average $ avg_2 = m_2 / c_2$ is calculated where $ m_2$ is the number of reads going through the window having at least $ avg_1$ or more reads connecting their border nodes and $ c_2$ the number of distinct pairs of border nodes having $ avg_1$ or more reads connecting them. Then, a read between two border nodes B and C is excluded if the number of reads going through B and C is less than or equal to $ limit$ given by

$\displaystyle limit = \frac{\log(avg_2)}{2} + \frac{avg_2}{16} $

An example where we resolve a repeat with conflicts is given in 28.9 where we have a total of 21 reads going through the window with $ avg_1 = 21 / 3 = 7$ , $ avg_2 = 20 / 2 = 10$ and $ limit = 1/2 + 10/16 = 1.125$ . Therefore all reads between border nodes B and C are excluded resulting in two sets of border nodes A, C and B, D. The resolved repeat is shown in figure 28.10.

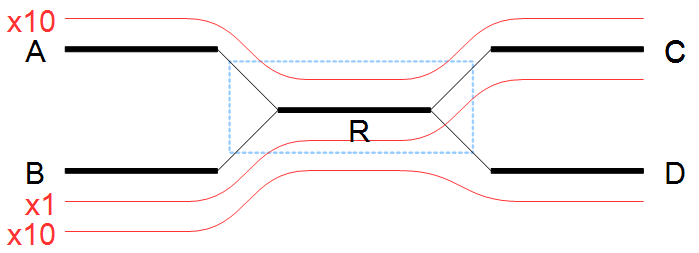
Image read_opt_3
Figure 28.9: A repeat with conflicts.

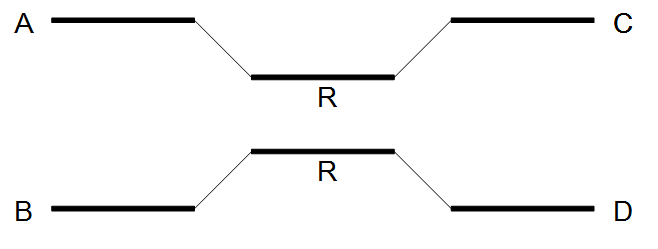
Image read_opt_4
Figure 28.10: Resolving a repeat with conflicts.