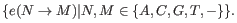The model for the Fixed Ploidy Variant Detection tool
The statistical model for the Fixed Ploidy Variant Detection tool consists of a model for the the possible site types,
- Prior site type probabilities:
- The set of possible site types is determined entirely by the assumed ploidy, and consists of the set of possible underlying nucleotide allele combinations that can exist within an individual with the specified number of alleles. E.g. if the specified ploidy is 2, the individual has two alleles, and the nucleotide at each allele can either be an
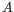 , a
, a 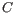 , a
, a 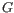 , a
, a 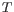 or a
or a  . The set of possible types for the diploid individual's sites is thus:
Note that, as we cannot distinguish the alleles from each other there are not 5
. The set of possible types for the diploid individual's sites is thus:
Note that, as we cannot distinguish the alleles from each other there are not 5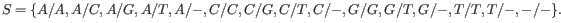
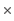 5 = 25 possible site types, but only 15 (that is, the allele combination
5 = 25 possible site types, but only 15 (that is, the allele combination 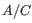 is indistinguishable from the allele combination
is indistinguishable from the allele combination 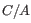 ).
).
We let
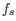 denote the prior probabilities of the site types
denote the prior probabilities of the site types 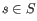 . The prior probabilities of the site types are the frequencies of the true site types in the mapping. The values of these are unknown, and need to be estimated from the data.
. The prior probabilities of the site types are the frequencies of the true site types in the mapping. The values of these are unknown, and need to be estimated from the data.
- Error probabilities:
- The model for the sequencing errors describes the probabilities with which the sequencing machine produces the nucleotide
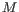 , when what it should have produced was the nucleotide
, when what it should have produced was the nucleotide 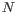 , (
, (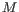 and
and 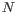
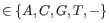 ). When quality values are available for the nucleotides in the reads, we let each quality value have its own error model; if not, a single model is assumed for all nucleotides. Each error model has the following 25 parameters:
The values of these parameters are also unknown, and hence also need to be estimated from the data.
). When quality values are available for the nucleotides in the reads, we let each quality value have its own error model; if not, a single model is assumed for all nucleotides. Each error model has the following 25 parameters:
The values of these parameters are also unknown, and hence also need to be estimated from the data.