The GLM model

Fitting a GLM to expression data

It is easiest to understand how the GLM model works through an example. Imagine an experiment looking at the effect of two drug treatments while controlling for gender:

In an abuse of mathematical notation, the underlying GLM for each gene looks like

$\displaystyle \log{y_i} = \mathrm{(placebo and Male)} + \mathrm{drugA} + \mathrm{drugB} + \mathrm{Female} + \mathrm{constant_i}$ (28.1)

where $ y_i$ is the expression level for the gene in sample $ i$; the combined term $ \mathrm{(placebo and Male)}$ describes an arbitrarily chosen baseline expression level (of males being given a placebo); and the other terms $ \mathrm{drugA}$, $ \mathrm{drugB}$ and $ \mathrm{Female}$ are numbers describing the effect of each group with respect to this baseline. The $ \mathrm{constant_i}$ accounts for differences in the library size between samples. For example, if a subject is male and given a placebo we predict the expression level to be

$\displaystyle \log{y_i} = \mathrm{(placebo and Male)} + \mathrm{constant_i}.$

If instead he had been given drug B, we would predict the expression level $ y_i$ to be augmented with the $ \mathrm{drugB}$ coefficient, resulting in

$\displaystyle \log{y_i} = \mathrm{(placebo and Male)} + \mathrm{drugB} + \mathrm{constant_i}.$

We assume that the expression levels $ y_i$ follow a Negative Binomial distribution. This distribution has a free parameter, the dispersion. The greater the dispersion, the greater the variation in expression levels for a gene.

The most likely values of the dispersion and coefficients, $ \mathrm{drugA}$, $ \mathrm{drugB}$ and $ \mathrm{Female}$, are determined simultaneously by fitting the GLM to the data. To see why this simultaneous fitting is necessary, imagine an experiment where we observe counts {3,10,4} for Males and {30,20,8} for Females. The most natural fit is for the coefficient $ \mathrm{Female}$ to have a two-fold change and for the dispersion to be small, but an alternative fit has no fold change and a larger dispersion. Under this second fit the variation in the counts is greater, and it is just by chance that all three Female values are larger than all three Male values.

Refining the estimate of dispersion

Much research has gone into refining the dispersion estimates of GLM fits. One important observation is that the GLM dispersion for a gene is often too low, because it is a sample dispersion rather than a population dispersion. We correct for this using the Cox-Reid adjusted likelihood, as in the multi-factorial edgeR method [Robinson et al., 2010]. 28.2

A second observation that can be used to improve the dispersion estimate, is that genes with the same average expression often have similar dispersions. To make use of this observation, we follow [Robinson et al., 2010] in estimating gene-wise dispersions from a linear combination of the likelihood for the gene of interest and neighboring genes with similar average expression levels. The weighting in this combination depends on the number of samples in an experiment, such that the neighbors have most weight when there are no replicates, and little effect when the number of replicates is high.

For dispersion, we used the following strategy:

  1. We sort the genes from lowest to highest averageLogCPM (CPM is defined also by the edgeR authors) For each gene, we calculate its loglikelihood at a grid of known dispersions. The known dispersions are 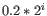$ 0.2 * 2^i$, where 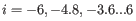$ i = { -6, -4.8, -3.6... 6 }$ such that there are 11 values of i in total. You can imagine the results of this as being stored in an array with one column for each gene and one row for each dispersion, with neighboring columns having similar averageLogCPM (because of the sorting in the previous step).

  2. We now calculate a weighted loglikelihood for each gene at these same known dispersions. This is the original loglikelihood for that gene at that dispersion plus a "weight factor" multiplied by the average loglikelihood for genes in a window of similar averageLogCPM. The window includes the 1.5% of genes to the left and to the right of the gene we are looking at. For example, if we had 3000 genes, and were calculating values for gene 500, then 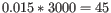$ 0.015*3000 = 45$, so we would average the values for genes 455 to 545. The "weight factor" = 20 / (numberOfSamples - number of parameters in the factor being tested). This means that the greater the number of samples, the lower the weight, and the fewer free parameters to fit, the lower the weight.

  3. We fit an FMM spline for each gene to its 11 weighted loglikelihoods. Our implementation of the FMM spline is translated from the Fortran code found here http://www.netlib.org/fmm/spline.f This spline allows us to estimate the weighted log-likelihood at any dispersion within the grid i.e., from 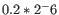$ 0.2 * 2^-6$ to $ 0.2*2^6$

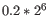
  4. We find the dispersion on the spline that maximizes the loglikelihood. This is the dispersion we use for that gene.

Statistical testing

The final GLM fit and dispersion estimate allows us to calculate the total likelihood of the model given the data, and the uncertainty on each fitted coefficient. The two statistical tests each make use of one of these values.

Wald test
Tests whether a given coefficient is non-zero. This test is used in the All group pairs and Against control group comparisons. For example, to test whether there is a difference between subjects treated with a placebo, and those treated with drugB, we would use the Wald test to determine if the 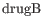$ \mathrm{drugB}$ coefficient is non-zero.
Likelihood Ratio test
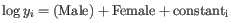Fits two GLMs, one with the given coefficients and one without. The more important the coefficients are, the greater the ratio of the likelihoods of the two models. This test is used in the Across groups (ANOVA-like) comparison. If we wanted to test whether either drug had an effect, we would compare the likelihoods of the GLM described in equation 28.1 with those in the reduced GLM $ \log{y_i} = \mathrm{(Male)} + \mathrm{Female} + \mathrm{constant_i}$.


Footnotes

...Robinson2010. 28.2
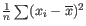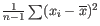To understand the purpose of the correction, it may help to consider the analogous situation of calculation of the variance of normally distributed measurements. One approach would be to calculate $ \frac{1}{n} \sum(x_i - \overline{x})^2$, but this is the sample variance and often too low. A commonly used correction for the population variance is: $ \frac{1}{n-1} \sum (x_i - \overline{x})^2$.