K-means/medoids clustering
In a k-means or medoids clustering, features are clustered into k separate clusters. The procedures seek to find an assignment of features to clusters, for which the distances between features within the cluster is small, while distances between clusters are large.
Toolbox | Microarray and Small RNA Analysis (![]() )| Feature Clustering | K-means/medoids Clustering (
)| Feature Clustering | K-means/medoids Clustering (![]() )
)
Select at least two samples ( (![]() ) or (
) or (![]() )) or an experiment (
)) or an experiment (![]() ).
).
Note! If your data contains many features, the clustering will take very long time and could make your computer unresponsive. It is recommended to perform this analysis on a subset of the data (which also makes it easier to make sense of the clustering). See how to create a sub-experiment in Creating sub-experiment from selection.
Clicking Next will display a dialog as shown in figure 29.67.
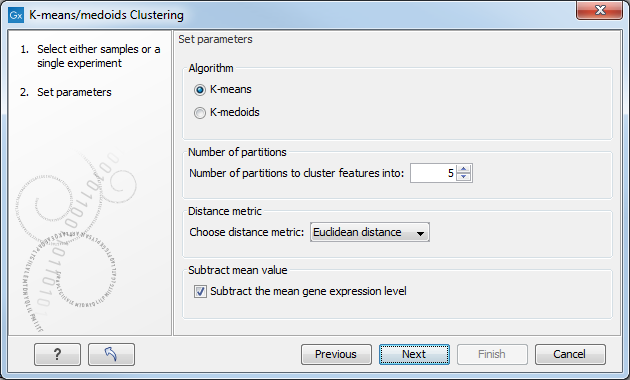
Figure 29.67: Parameters for k-means/medoids clustering.
The parameters are:
- Algorithm. You can choose between two clustering methods:
- K-means. K-means clustering assigns each point to the cluster whose center is nearest. The center/centroid
of a cluster is defined as the average of all points in the cluster. If a data set has three dimensions and the
cluster has two points
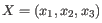 and
and
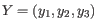 , then the centroid
, then the centroid  becomes
becomes
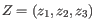 , where
, where
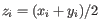 for
for 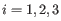 .
The algorithm attempts to minimize the intra-cluster variance defined by:
where there are
.
The algorithm attempts to minimize the intra-cluster variance defined by:
where there are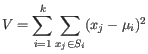
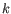 clusters
clusters
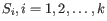 and
and 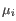 is the centroid of all points
is the centroid of all points
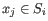 . The detailed algorithm can be found in [Lloyd, 1982].
. The detailed algorithm can be found in [Lloyd, 1982].
- K-medoids. K-medoids clustering is computed using the PAM-algorithm (PAM is short for Partitioning Around Medoids). It chooses datapoints as centers in
contrast to the K-means algorithm. The PAM-algorithm is based on the search for
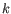 representatives (called medoids) among all elements of the dataset. When having found
representatives (called medoids) among all elements of the dataset. When having found
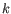 representatives
representatives 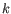 clusters are now generated by assigning each element to its nearest medoid. The algorithm first looks for a good initial set of medoids
(the BUILD phase). Then it finds a local minimum for the
objective function:
where there are
clusters are now generated by assigning each element to its nearest medoid. The algorithm first looks for a good initial set of medoids
(the BUILD phase). Then it finds a local minimum for the
objective function:
where there are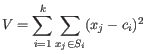
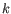 clusters
clusters
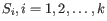 and
and 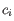 is the medoid of
is the medoid of 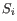 . This solution implies that there is no single switch of an object with a
medoid that will decrease the objective (this is called the SWAP phase). The PAM-agorithm is described in [Kaufman and Rousseeuw, 1990].
. This solution implies that there is no single switch of an object with a
medoid that will decrease the objective (this is called the SWAP phase). The PAM-agorithm is described in [Kaufman and Rousseeuw, 1990].
- K-means. K-means clustering assigns each point to the cluster whose center is nearest. The center/centroid
of a cluster is defined as the average of all points in the cluster. If a data set has three dimensions and the
cluster has two points
- Number of partitions. The maximum number of partitions to cluster features into: the final number of clusters can be smaller than that.
- Distance metric. The metric to compute distance between data points.
- Euclidean distance. The ordinary distance between two elements - the length of the segment connecting them. If
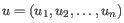 and
and
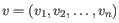 ,
then the Euclidean distance between
,
then the Euclidean distance between 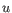 and
and 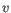 is
is

- Manhattan distance. The Manhattan distance between two elements is the distance measured along axes at right angles. If
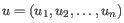 and
and
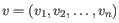 ,
then the Manhattan distance between
,
then the Manhattan distance between 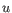 and
and 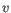 is
is
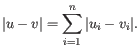
- Euclidean distance. The ordinary distance between two elements - the length of the segment connecting them. If
- Subtract mean value. For each gene, subtract the mean gene expression value over all input samples.
Clicking Next will display a dialog as shown in figure 29.68.
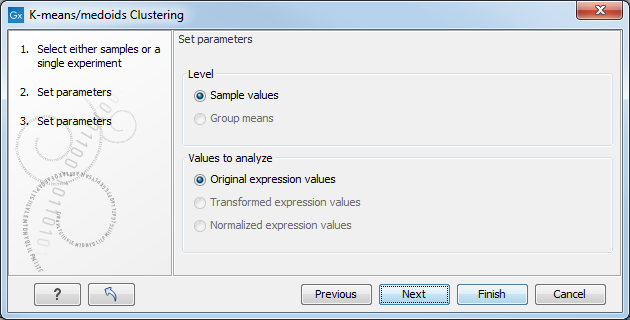
Figure 29.68: Parameters for k-means/medoids clustering.
At the top, you can choose the Level to use. Choosing 'sample values' means that distances will be calculated using all the individual values of the samples. When 'group means' are chosen, distances are calculated using the group means.
At the bottom, you can select which values to cluster (see Selecting transformed and normalized values for analysis).
Click Finish to start the tool.
The k-means implementation first assigns each feature to a cluster at random. Then, at each iteration, it reassigns features to the centroid of the nearest cluster. During this reassignment, it can happen that one or more of the clusters becomes empty, explaining why the final number of clusters might be smaller than the one specified in "number of partitions". Note that the initial assignment of features to clusters is random, so results can differ when the algorithm is run again.
Subsections
