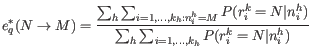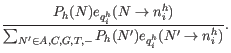Updating equations for the error rates
Consider a site ![]() and a read
and a read ![]() . The joint probability of the true nucleotide in the read,
. The joint probability of the true nucleotide in the read, ![]() , at the site being
, at the site being ![]() and the observed nucleotide at the site
and the observed nucleotide at the site ![]() is:
is:
Using Bayes Theorem, the probability of the true nucleotide in the read, ![]() , at the site being
, at the site being ![]() , given that we observe
, given that we observe ![]() is:
is:
Inserting 28.15 in 28.16 we get:
The equation 28.17 gives us the probabilities for a given read, ![]() , and site,
, and site, ![]() , given the observed nucleotide
, given the observed nucleotide ![]() , that the true nucleotide is
, that the true nucleotide is ![]() ,
,
![]() , given our current values for the frequency
, given our current values for the frequency ![]() (inserted for
(inserted for ![]() ) and error rates. Since we know the sequenced nucleotide in each read at each site, we can get new updated values for the error rate of producing an
) and error rates. Since we know the sequenced nucleotide in each read at each site, we can get new updated values for the error rate of producing an ![]() nucleotide when the true nucleotide is
nucleotide when the true nucleotide is ![]() ,
,
![]() , for
, for
![]() by summing the probabilities of the true nucleotide being
by summing the probabilities of the true nucleotide being ![]() for all reads across all sites for which the sequenced nucleotide is
for all reads across all sites for which the sequenced nucleotide is ![]() , and dividing by the sum of all probabilities of the true nucleotide being a
, and dividing by the sum of all probabilities of the true nucleotide being a ![]() across all reads and all sites:
across all reads and all sites: