The velocity estimation algorithm

The velocity estimation algorithm closely follows the approach implemented in scVelo [Bergen et al., 2020] and it contains multiple steps, covering different scVelo methods:

  1. Genes are filtered such that only the genes that are HVGs (if used) and have a sufficient spliced and unspliced count are retained for the velocity calculations. Spliced and unspliced counts are then normalized to correct for sequencing depth. Each type of count is divided by the total observed count of the cell, and multiplied to the median total count across all cells. The total counts are obtained by summing over the genes retained for the velocity calculations.
  2. A k-nearest neighbor graph is calculated using the pairwise Euclidean distance between all cells, using either the raw or normalized, if available, total gene expression, after any optional HVGs selection and dimensionality reduction. Using each cell's nearest neighbors, the spliced and unspliced counts are imputed as the average normalized spliced and unspliced counts across the neighborhood.
  3. Velocity is estimated for each gene according to the chosen model:
    • Steady-state model: A linear regression on the extreme quantiles of the spliced and unspliced counts is used to determine the steady-state ratio. Genes are considered velocity genes if the inferred ratio and 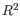$ R^2$ are above $ 0.01$.
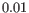    • Dynamical model: To reduce computational cost, the dynamical model is only estimated for genes that are considered velocity genes based on the steady-state model. If the gene likelihood is larger than 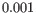$ 0.001$, the gene is considered a velocity gene.

    Downstream analysis is only performed using the velocity genes.

  4. Transition probabilities are calculated from the cosine similarity, which measures how well the change in gene expression can be explained by the estimated velocity vector.
  5. Velocity coherence (how a velocity vector correlates with its neighboring velocities) and length (speed or rate of differentiation) are calculated for each cell.
  6. If the dynamical model was used, the gene-shared latent time representing the cells' internal clocks is estimated by using the inferred dynamics.

    Note that inference of the terminal states requires calculating the eigenvector of the transition probability matrix corresponding to an eigenvalue 1. If the estimated eigenvalue is not sufficiently close to 1, the resulting terminal states are not trustworthy and hence the latent time is not calculated.

The above steps are equivalent to running the following commands in scVelo 0.2.4: 

import scVelo as scv
scv.pp.filter_and_normalize(adata, min_shared_counts=20, n_top_genes=2000)
scv.pp.moments(adata, n_neighbors=30, n_pcs=20)
# only for the steady-state model
scv.tl.velocity(adata, mode='deterministic')
# only for the dynamical model
scv.tl.recover_dynamics(adata) 
scv.tl.velocity(adata, mode='dynamical')
scv.tl.velocity_graph(adata)
scv.tl.get_transition_matrix(adata, scale=10, self_transitions=True, use_negative_cosines=True)
scv.tl.velocity_confidence(adata)
# only for the dynamical model
scv.tl.latent_time(adata)

Note that small differences to scVelo are expected in the results due to the different normalized total gene expression. Additionally, the dynamical model uses numerical optimization and this can lead to different estimated kinetic parameters and hence estimated velocities.