Structure elements and their energy contribution
In this section, we classify the structure elements defining a secondary structure and describe their energy contribution.
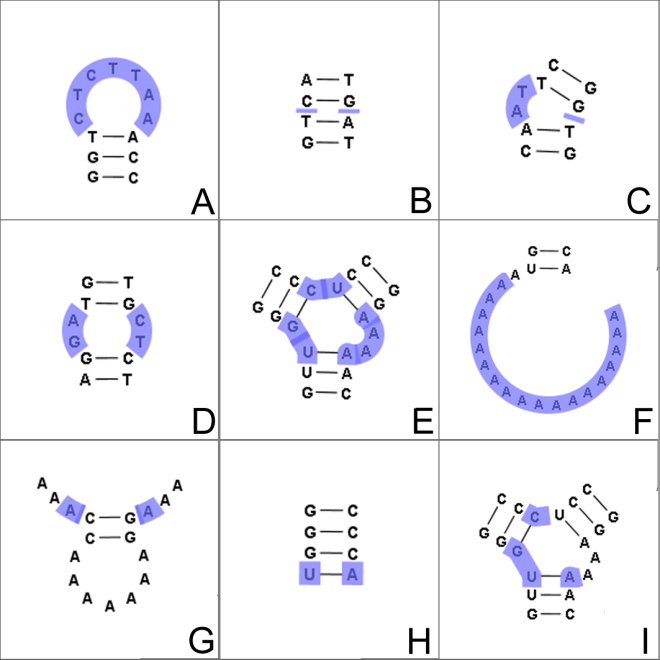
Figure 22.29: The different structure elements of RNA secondary structures predicted with the free energy minimization algorithm in CLC Main Workbench. See text for a detailed description.
Nested structure elements
The structure elements involving nested base pairs can be classified by a given base pair and the other base pairs that are nested and accessible from this pair. For a more elaborate description we refer the reader to [Sankoff et al., 1983] and [Zuker and Sankoff, 1984].
If the nucleotides with position number 
form a base pair
and
, then we say that the base pair 
is
accessible from if there is no intermediate base pair
such that
. This means that is nested within the pair 
and there is no other base pair
in between.
Using the number of accessible pase pairs, we can define the following distinct structure elements:
- Hairpin loop (
). A base pair with 0 other accessible base pairs forms a hairpin loop. The energy
contribution of a hairpin is determined by the length of the
unpaired (loop) region and the two bases adjacent to the closing
base pair which is termed a terminal mismatch (see figure 22.29A).
- A base pair with 1 accessible base pair can give rise to three distinct structure elements:
- Stacking of base pairs (
). A stacking of two consecutive pairs occur if
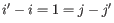. Only canonical base pairs (
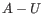or 
or
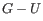) are allowed (see figure 22.29B). The energy contribution is determined by the
type and order of the two base pairs.
- Bulge (
). A bulge loop occurs if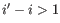 
or
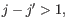but not both. This means that the two base pairs enclose an unpaired region of length 0 on one side and
an unpaired region of length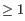 
on the other side (see figure 22.29C). The energy
contribution of a bulge is determined by the length of the
unpaired (loop) region and the two closing base pairs.
- Interior loop (
).An interior loop occurs if both 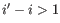and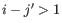 
This means that the two base pairs enclose an unpaired region of length 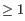on both sides (see figure 22.29D). The energy contribution of an interior loop is
determined by the length of the
unpaired (loop) region and the four unpaired bases adjacent to the opening- and the closing
base pair.
- Stacking of base pairs (
- Multi loop opened (
). A base pair with more than two accessible base pairs gives rise to a multi loop, a loop from which three or more stems are
opened (see figure 22.29E). The energy contribution of a multi loop depends on the
number of Stems opened in multi-loop (
) that protrude from the loop.
Other structure elements
- A collection of single stranded bases not accessible from any base
pair is called an exterior (or external) loop (see figure 22.29F). These regions do not
contribute to the total free energy.
- Dangling nucleotide (
). A dangling nucleotide is
a single stranded nucleotide that forms a stacking interaction with
an adjacent base pair. A dangling nucleotide can be a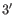 
or
-dangling nucleotide depending on the orientation (see figure 22.29G). The energy
contribution is determined by the single stranded nucleotide, its
orientation and on the adjacent base pair.
- Non-GC terminating stem (
). If a base pair other than a G-C pair is found at the end of a stem, an energy penalty is assigned (see figure 22.29H).
- Coaxial interaction (
). Coaxial stacking is a favorable interaction of two stems where the base pairs at the ends can form a stacking interaction.
This can occur between stems in a multi loop and between the stems of two different
sequential structures. Coaxial stacking can occur between stems with no intervening nucleotides (adjacent
stems) and between stems with one intervening nucleotide from each
strand (see figure 22.29I). The energy contribution is determined by the adjacent base
pairs and the intervening nucleotides.
Experimental constraints
A number of techniques are available for probing RNA structures. These techniques can determine individual components of an existing structure such as the existence of a given base pair. It is possible to add such experimental constraints to the secondary structure prediction based on free energy minimization (see figure 22.30) and it has been shown that this can dramatically increase the fidelity of the secondary structure prediction [Mathews and Turner, 2006].
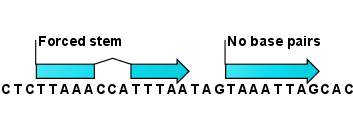
Figure 22.30: Known structural features can be added as constraints to the secondary structure prediction algorithm in CLC Main Workbench.