Refining the estimate of dispersion

Much research has gone into refining the dispersion estimates of GLM fits. One important observation is that the GLM dispersion for a gene is often too low, because it is a sample dispersion rather than a population dispersion. We correct for this using the Cox-Reid adjusted likelihood, as in the multi-factorial EdgeR method [Robinson et al., 2010]. 29.2

A second observation that can be used to improve the dispersion estimate, is that genes with the same average expression often have similar dispersions. To make use of this observation, we follow [Robinson et al., 2010] in estimating genewise dispersions from a linear combination of the likelihood for the gene of interest and neighboring genes with similar average expression levels. The weighting in this combination depends on the number of samples in an experiment, such that the neighbors have most weight when there are no replicates, and little effect when the number of replicates is high.


Footnotes

...Robinson2010. 29.2
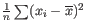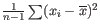To understand the purpose of the correction, it may help to consider the analogous situation of calculation of the variance of normally distributed measurements. One approach would be to calculate $ \frac{1}{n} \sum(x_i - \overline{x})^2$, but this is the sample variance and often too low. A commonly used correction for the population variance is: $ \frac{1}{n-1} \sum (x_i - \overline{x})^2$.