Resolve repeats using reads

Having build the de Bruijn graph using words, our de novo assembler removes repeats and errors using reads. This is done in the following order: Each phase will be explained in the following.

Remove weak edges The de Bruijn graph is expected to contain artifacts from errors in the data. The number of reads agreeing upon an error is likely to be low especially compared to the number of reads without errors for the same region. When this relative difference is large enough, it's possible to conclude something is an error.

In the remove weak edges phase we consider each node and calculate the number $ c_1$ of edges connected to the node and the number of times $ k_1$ a read is passing through these edges. An average of reads going through an edge is calculated $ avg_1 = k_1 / c_1$ and then the process is repeated using only those edges which have more than or equal $ avg_1$ reads going though it. Let $ c_2$ be the number of edges which meet this requirement and $ k_2$ the number of reads passing through these edges. A second average $ avg_2 = k_2 / c_2$ is used to calculate a limit,

$\displaystyle limit = \frac{\log(avg_2)}{2} + \frac{avg_2}{40} $

and each edge connected to the node which has less than or equal $ limit$ number of reads passing through it will be removed in this phase.

Remove dead ends Some read errors might occur more often than expected, either by chance or because they are systematic sequencing errors. These are not removed by the "Remove weak edges" phase and will cause "dead ends" to occur in the graph, which are short paths in the graph that terminate after a few nodes. Furthermore, the "Remove weak edges" sometimes only removes a part of the graph, which will also leave dead ends behind. Dead ends are identified by searching for paths in the graph where there exits an alternative path containing four times more nucleotides. All nodes in such paths are then removed in this step.

Resolve repeats without conflicts Repeats and other shared regions between the reads lead to ambiguities in the graph. These must be resolved otherwise the region will be output as multiple contigs, one for each node in the region.

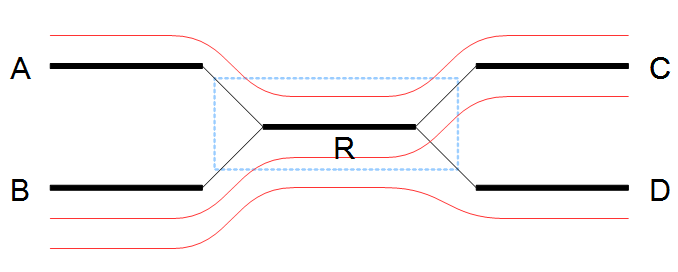
The algorithm for resolving repeats without conflicts considers a number of nodes called the window. To start with, a window only contains one node, say R. We also define the border nodes as the nodes outside the window connected to a node in the window. The idea is to divide the border nodes into sets such that border nodes A and C are in the same set if there is a read going through A, through nodes in the window and then through C. If there are strictly more than one of these sets we can resolve the repeat area, otherwise we expand the window.

Image read_opt_1
Figure 35.6: A set of nodes.

In the example in figure 35.6 all border nodes A, B, C and D are in the same set since one can reach every border nodes using reads (shown as red lines). Therefore we expand the window and in this case add node C to the window as shown in figure 35.7.

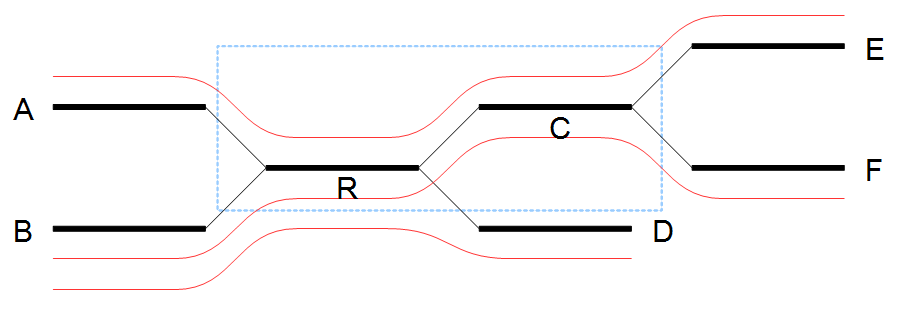
Image read_opt_2
Figure 35.7: Expanding the window to include more nodes.

After the expansion of the window, the border nodes will be grouped into two groups being set A, E and set B, D, F. Since we have strictly more than one set, the repeat is resolved by copying the nodes and edges used by the reads which created the set. In the example the resolved repeat is shown in figure 35.8.

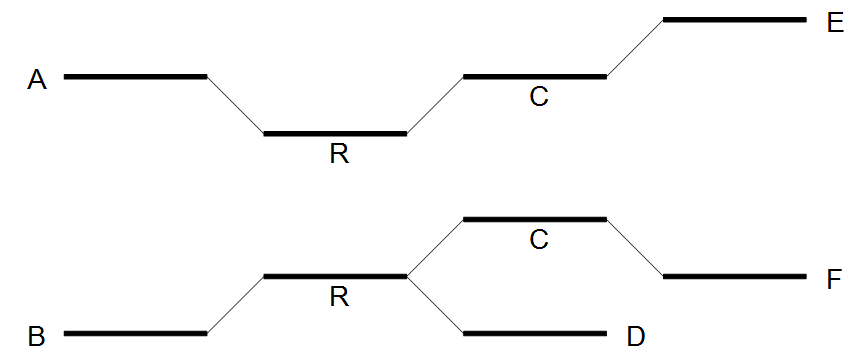
Image read_opt_5
Figure 35.8: Resolving the repeat.

The algorithm for resolving repeats without conflict can be described the following way:

  1. A node is selected as the window
  2. The border is divided into sets using reads going through the window. If we have multiple sets, the repeat is resolved.
  3. If the repeat cannot be resolved, we expand the window with nodes if possible and go to step 2.
The above steps are performed for every node.

Resolve repeats with conflicts In the previous section repeats were resolved without excluding any reads that goes through the window. While this lead to a simpler graph, the graph will still contain artifacts, which have to be removed. The next phase removes most of these errors and is similar to the previous phase:

  1. A node is selected as the initial window
  2. The border is divided into sets using reads going through the window. If we have multiple sets, the repeat is resolved.
  3. If the repeat cannot be resolved, the border nodes are divided into sets using reads going through the window where reads containing errors are excluded. If we have multiple sets, the repeat is resolved.
  4. The window is expanded with nodes if possible and step 2 is repeated.

The algorithm described above is similar to the algorithm used in the previous section, except step 3 where the reads with errors are excluded. This is done by calculating an average $ avg_1 = m_1 / c_1$ where $ m_1$ is the number of reads going through the window and $ c_1$ is the number of distinct pairs of border nodes having one (or more) of these reads connecting them. A second average $ avg_2 = m_2 / c_2$ is calculated where $ m_2$ is the number of reads going through the window having at least $ avg_1$ or more reads connecting their border nodes and $ c_2$ the number of distinct pairs of border nodes having $ avg_1$ or more reads connecting them. Then, a read between two border nodes B and C is excluded if the number of reads going through B and C is less than or equal to $ limit$ given by

$\displaystyle limit = \frac{\log(avg_2)}{2} + \frac{avg_2}{16} $

An example where we resolve a repeat with conflicts is given in 35.9 where we have a total of 21 reads going through the window with $ avg_1 = 21 / 3 = 7$, $ avg_2 = 20 / 2 = 10$ and $ limit = 1/2 + 10/16 = 1.125$. Therefore all reads between border nodes B and C are excluded resulting in two sets of border nodes A, C and B, D. The resolved repeat is shown in figure 35.10.

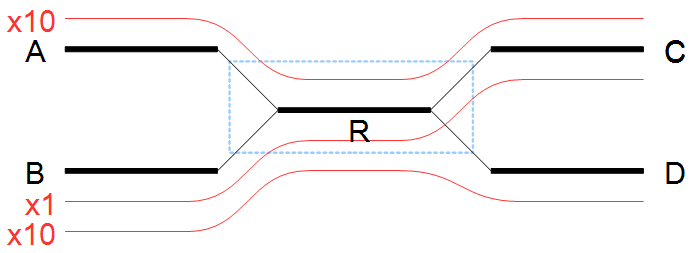
Image read_opt_3
Figure 35.9: A repeat with conflicts.

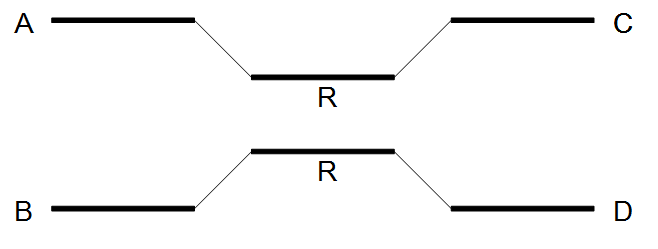
Image read_opt_4
Figure 35.10: Resolving a repeat with conflicts.