QIAGEN Bioinformatics Manuals

The Normalize Single Cell Data algorithm

The algorithm is based on sctransform v2 [Hafemeister and Satija, 2019,Choudhary and Satija, 2022]. Briefly:

5000 cells are randomly sampled.
2000 genes are uniformly sampled across a range of expressions. Genes expressed in fewer than 5 sampled cells are excluded.
A generalized linear model (GLM) is fitted to each gene using the sampled cells. Genes with an arithmetic mean expression of less than 0.001, or a variance lower than the arithmetic mean, are modeled using a Poisson GLM; otherwise, a negative binomial (NB) GLM is used.

The form of the GLM is:

$\displaystyle \log{\mathbb{E}(y_i)} = \beta_0 + \ln{m_i} ,$

where $\beta_0$ is the intercept and is the observed expression for the gene for a cell that has total expression .

The dispersion parameter $\gamma = 1/\theta$ of the NB distribution is estimated using the Cox-Reid penalized adjusted likelihood [Robinson et al., 2010]. The NB distribution reduces to the Poisson distribution when $\gamma=0$ ( $\theta = \infty$ ).

LOWESS regression is used to estimate $\beta_0$ and $\gamma$ as a function of the average expression. This acts as a form of regularization, preventing over-fitting, particularly for genes with low expression levels.

The algorithm is adjusted as follows when batch correction is applied:

5000 cells are randomly sampled per batch. For example, in data prepared by two investigators using multiple technologies, where batch correction aims to remove both of these effects, up to 5000 cells are sampled for each combination of investigator and technology.
A GLM is fitted to every gene, as any gene could exhibit a batch effect. Genes expressed in fewer than 5 sampled cells are excluded.
Batch effect terms are added to the model. These terms cannot be regularized because each gene may exhibit a batch effect that differs from those of genes with similar expression levels.
Regularization is applied only to 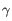$\gamma$ , as mixing regularized and non-regularized terms would create results that cannot be disentangled. Consequently, batch correction tends to over-correct the data. However, this issue diminishes as the data size increases.

Normalized values are Pearson residuals, representing the portion of expression that is not explained by the model fit. For each gene, these are defined as follows:

$\displaystyle z_i$	$\displaystyle = \frac{y_i - \exp{(\beta_0 + \ln{m_i})}}{\sigma}$
	$\displaystyle = \frac{y_i - \hat{y_i}}{\sigma}$
	$\displaystyle = \frac{y_i - \hat{y_i}}{\sqrt{\hat{y_i}(1+\gamma\hat{y_i})}}$

Note that Pearson residuals have the following properties that may be unexpected. They are:

Decimals (e.g., 123.4) rather than integers (e.g., 123).
Negative, though typically not very negative, when the expression of a gene in a cell is lower than predicted by the GLM. Negative (though typically not very negative) when the gene expression in a cell is lower than predicted by the GLM.
Zero for all cells in the unlikely event that expression can be perfectly predicted by the GLM.
Only defined within the context of a specific dataset and cannot be compared across datasets. For example, for three datasets A, B, and C, running the tool on A and B might lead to a normalized expression of 100 for a particular cell and gene in data A, whereas running the same tool on A and C might lead to a normalized expression of 0 for the same cell and gene.

Browse the manual

The Normalize Single Cell Data algorithm