K-mer based distance estimation
K-mer based distance estimation is an alternative to estimating
evolutionary distance based on multiple alignments. At a high level, the distance
between two sequences is defined by first collecting the set of k-mers (subsequences of length k)
occuring in the two
sequences. From these two sets, the evolutionary distance between the
two organisms is now defined by measuring how different the two sets are. The more the two sets look alike, the smaller is the
evolutionary distance. The main motivation for estimating evolutionary
distance based on k-mers, is that it is computationally much faster
than first constructing a multiple alignment. Experiments show
that phylogenetic tree reconstruction using k-mer based distances
can produce results comparable to the slower multiple alignment based
methods [Blaisdell, 1989].
All of the k-mer based distance measures completely ignores the ordering of
the k-mers inside the input sequences. Hence, if the selected k value (the length of the sequences) is too
small, very distantly related organisms may be assigned a small
evolutionary distance (in the extreme case where k is ![]() , two organisms will
be treated as being identical if the frequency of each
nucleotide/amino-acid is the same in the two corresponding
sequences). In the other extreme, the k-mers should have a length (k) that
is somewhat below the average distance between mismatches if the input
sequences were aligned (in the extreme case of k=the length of the
sequences, two organisms have a maximum distance if they are not
identical). Thus the selected k value should not be too large and not too
small. A general rule of thumb is to only use k-mer based distance
estimation for organisms that are not too distantly related.
, two organisms will
be treated as being identical if the frequency of each
nucleotide/amino-acid is the same in the two corresponding
sequences). In the other extreme, the k-mers should have a length (k) that
is somewhat below the average distance between mismatches if the input
sequences were aligned (in the extreme case of k=the length of the
sequences, two organisms have a maximum distance if they are not
identical). Thus the selected k value should not be too large and not too
small. A general rule of thumb is to only use k-mer based distance
estimation for organisms that are not too distantly related.
Formal definition of distance. In the following, we give a more
formal definition of the three supported distance measures:
Euclidian-squared, Mahalanobis and Fractional common k-mer count. For
all three, we first
associate a point ![]() to every input sequence
to every input sequence ![]() . Each point
. Each point
![]() has one coordinate for every possible length k sequence (e.g. if
has one coordinate for every possible length k sequence (e.g. if ![]() represent nucleotide sequences, then
represent nucleotide sequences, then ![]() has
has ![]() coordinates). The coordinate
corresponding to a length k sequence
coordinates). The coordinate
corresponding to a length k sequence ![]() has the value: "number of
times
has the value: "number of
times ![]() occurs as a subsequence in
occurs as a subsequence in ![]() ". Now for two sequences
". Now for two sequences
![]() and
and ![]() , their evolutionary distance is defined as follows:
, their evolutionary distance is defined as follows:
- Euclidian squared: For this measure, the distance is
simply defined as the
(squared Euclidian) distance between the two points
 and
and  ,
i.e.
,
i.e. 
- Mahalanobis: This measure is essentially a fine-tuned
version of the Euclidian squared distance measure. Here all the
counts
 are "normalized" by dividing with the standard
deviation
are "normalized" by dividing with the standard
deviation  of
the count for the k-mer. The revised formula thus becomes:
Here the standard deviations can be computed directly from a set of equilibrium frequencies for the different bases, see [Gentleman and Mullin, 1989].
of
the count for the k-mer. The revised formula thus becomes:
Here the standard deviations can be computed directly from a set of equilibrium frequencies for the different bases, see [Gentleman and Mullin, 1989].
- Fractional common k-mer count: For the last measure,
the distance is computed based on the minimum count of every k-mer
in the two sequences, thus if two sequences are very different, the
minimums will all be small. The formula is as follows:
Here

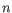 is the length of
is the length of  and
and  is the length of
is the length of  . This
method has been described in [Edgar, 2004].
. This
method has been described in [Edgar, 2004].
In experiments performed in [Höhl et al., 2007], the Mahalanobis distance measure seemed to be the best performing of the three supported measures.
