Hierarchical clustering of features

A hierarchical clustering of features is a tree presentation of the similarity in expression profiles of the features over a set of samples (or groups). The tree structure is generated by

letting each feature be a cluster
calculating pairwise distances between all clusters
joining the two closest clusters into one new cluster
iterating 2-3 until there is only one cluster left (which will contain all samples).

The tree is drawn so that the distances between clusters are reflected by the lengths of the branches in the tree. Thus, features with expression profiles that closely resemble each other have short distances between them, those that are more different, are placed further apart.

To start the clustering of features:

Toolbox | Transcriptomics Analysis ()| Feature Clustering | Hierarchical Clustering of Features ()

Select at least two samples ( () or ()) or an experiment ().

Note! If your data contains many features, the clustering will take very long time and could make your computer unresponsive. It is recommended to perform this analysis on a subset of the data (which also makes it easier to make sense of the clustering. Typically, you will want to filter away the features that are thought to represent only noise, e.g. those with mostly low values, or with little difference between the samples). See how to create a sub-experiment in Creating sub-experiment from selection.

Clicking Next will display a dialog as shown in figure 28.94. The hierarchical clustering algorithm requires that you specify a distance measure and a cluster linkage. The distance measure is used specify how distances between two features should be calculated. The cluster linkage specifies how you want the distance between two clusters, each consisting of a number of features, to be calculated.

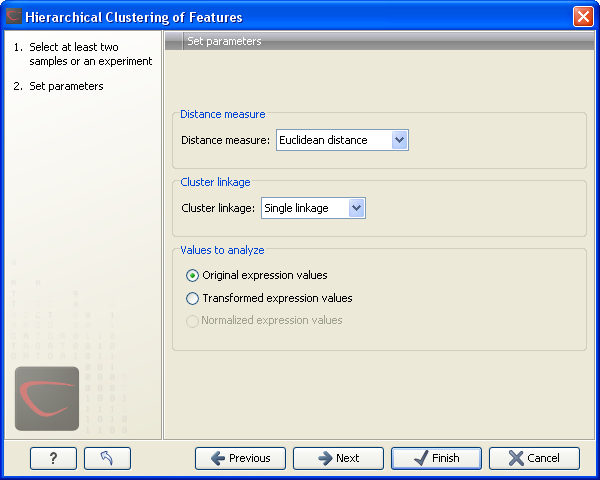
Image feature_clustering_step2
Figure 28.93: Parameters for hierarchical clustering of features.

At the top, you can choose three kinds of Distance measures:

Euclidean distance. The ordinary distance between two points - the length of the segment connecting them. If $u=(u_1,u_2,\dots, u_n)$ and $v=(v_1,v_2,\dots, v_n)$ , then the Euclidean distance between and is

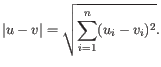
$\displaystyle \vert u-v\vert = \sqrt{\sum_{i=1}^n (u_i-v_i)^2}.$
1 - Pearson correlation. The Pearson correlation coefficient between two elements and is defined as

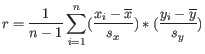
$\displaystyle r = \frac{1}{n-1}\sum_{i=1}^n (\frac{x_i-\overline{x}}{s_x})*(\frac{y_i-\overline{y}}{s_y})$
where $\overline{x}/\overline{y}$ is the average of values in and is the sample standard deviation of these values. It takes a value $\in [-1,1]$ . Highly correlated elements have a high absolute value of the Pearson correlation, and elements whose values are un-informative about each other have Pearson correlation 0. Using $1-\vert Pearson correlation\vert$ as distance measure means that elements that are highly correlated will have a short distance between them, and elements that have low correlation will be more distant from each other.
Manhattan distance. The Manhattan distance between two points is the distance measured along axes at right angles. If $u=(u_1,u_2,\dots, u_n)$ and $v=(v_1,v_2,\dots, v_n)$ , then the Manhattan distance between and is

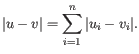
$\displaystyle \vert u-v\vert = \sum_{i=1}^n \vert u_i-v_i\vert.$

Next, you can select different ways to calculate distances between clusters. The possible cluster linkage to use are:

Single linkage. The distance between two clusters is computed as the distance between the two closest elements in the two clusters.
Average linkage. The distance between two clusters is computed as the average distance between objects from the first cluster and objects from the second cluster. The averaging is performed over all pairs , where is an object from the first cluster and is an object from the second cluster.
Complete linkage. The distance between two clusters is computed as the maximal object-to-object distance , where comes from the first cluster, and comes from the second cluster. In other words, the distance between two clusters is computed as the distance between the two farthest objects in the two clusters.

At the bottom, you can select which values to cluster (see Selecting transformed and normalized values for analysis). Click Next if you wish to adjust how to handle the results. If not, click Finish.

Subsections

Result of hierarchical clustering of features